Media

La media, también conocida como media aritmética o promedio, es un término que se utiliza en la estadística para determinar la tendencia central de una serie de datos con respecto a un parámetro específico.

Es decir, es una cantidad que resulta de dividir la suma de los valores de todas las observaciones entre el número total de esas observaciones realizadas. Para ello, se suman los elementos del conjunto y se obtiene el cociente entre el total de ellos.

Este elemento matemático es muy aplicado en el ámbito académico, laboral o profesional. Además, las instituciones u organismos oficiales que dan a conocer promedios o tendencias, se valen de la media para organizar sus datos. De hecho, es el término más empleado para hacer comparaciones entre distintas muestras poblacionales en distintas áreas de investigación.

Tipos

Aunque la media aritmética es la que más se utiliza en los cálculos estadísticos, también existen otros tipos de media, como por ejemplo:

Media ponderada

En ella se emplean números denominados pesos o valores para dar más sustentación a determinados datos. Es una metodología que se emplea con frecuencia en los cálculos académicos y en los índices referenciales para una población.

Su principal diferencia con respecto a la media aritmética es que en ella todos los valores no tienen la misma importancia o ponderación.

Media geométrica

Este tipo de media se basa en el cálculo total de un conjunto de productos. Por lo tanto, si algún componente del conjunto es igual a cero, el resultado de la media geométrica también lo será.

Es un término muy útil para calcular porcentajes o puntuaciones, ya que no es tan sensible a los valores de los extremos.

Media cuadrática

La media cuadrática sirve para calcular promedios, tanto de datos positivos como negativos. Es el cálculo de la raíz cuadrado de los elementos al cuadrado.

Se trata de un tipo de media que se emplea con mucha frecuencia en distintas áreas del conocimiento y del manejo de datos, puesto que no importa si el valor es negativo, ya que solo se toma el valor absoluto resultante.

Media armónica

Esta media se emplea para el cálculo de índices, velocidades y tiempo. Expresa la relación recíproca entre las unidades. Eso sí, no se puede calcular si alguno de sus valores es igual a cero.

Fórmulas y cálculo

A continuación, se presentan las fórmulas y la manera de calcular cada una de las medias, incluida la media aritmética:

Cálculo de la media aritmética

Esta media es de gran utilidad porque permite expresar rápidamente una tendencia central. Su cálculo se basa en la suma de los datos entre el total del número de evento. Por ejemplo:

Las notas del lapso académico fueron: 15, 10, 18, 20.

Se puede ver que son 4 materias en total. Por lo tanto, la media aritmética se obtiene de sumar las cuatro notas y dividirlas entre 4, lo que da como resultado un promedio de 16 puntos.

Cálculo de la media ponderada

Esta media se calcula tomando el conjunto de elementos (Xi, X2, X3…) y el peso de los datos (w1, w2…). Luego, se aplica la siguiente fórmula:

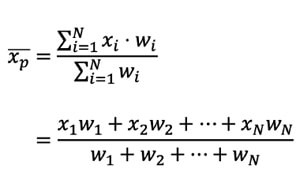
X: Representa a los valores de cada elemento.

W: son los valores ponderados.

Por ejemplo, en una asignatura un examen tenía una ponderación 4 y otro de 6. Las notas que obtuvo el estudiante respectivamente fueron de 15 y 20. Para obtener la media ponderada se multiplican y dividen los datos de la siguiente manera:

Media ponderada: (15 x 4) + (20 x 6) / (6+4) = 18

Cálculo de la media geométrica

Para calcular esta media, todos los elementos del conjunto deben ser distintos de cero. Se aplica la siguiente fórmula:

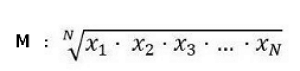
M: es la media geométrica a calcular.

X: Se trata de cada uno de los valores.

Los ejercicios al multiplicar los datos y al resultado se le aplica la raíz con el índice correspondiente al total de los eventos.

Cálculo de la media cuadrática

A esta media también se le conoce como RMS y se calcula con la siguiente fórmula matemática:

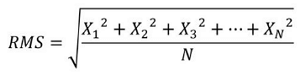
X: representa cada uno de los valores, pero elevados al cuadrado.

Un ejemplo simple de la media cuadrática es cuando un grupo de 7 estudiantes realizan un experimento y desean calcular el error en sus medidas.

Para ello, solo toman las desviaciones estándar de cada uno, las elevan al cuadrado, aplican la suma de todas y buscan el cociente entre el total de las desviaciones, que en este caso son 7.

Por último, aplican la raíz cuadrada para el resultado final.

Cálculo de la media armónica

Se calcula conociendo los inversos de los datos numéricos y utilizando la siguiente fórmula:

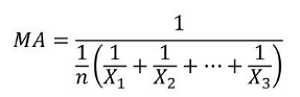
N: es el total de los eventos.

X: es cada uno de los valores, pero colocados como denominador.

Cada una de estas medias es de gran utilidad para el cálculo de promedios y variabilidades, ya que son poco sensibles a los extremos y desviaciones. Además, sus medidas permiten comparar las tendencias con respecto a un dato central.

Conceptos relacionados: moda, mediana

Además de la media, en estadística existen otros conceptos que son esenciales para validar y organizar la información:

Mediana

Se trata de una relación estadística que organiza los datos en proporciones iguales en ambos extremos del ejercicio. Es decir, al momento de presentar la información, organiza los datos de mayor a menor y muestra el punto central.

Por lo general, se trata de valores enteros y que se pueden calcular aunque el límite de los datos propuestos tienda al infinito.

El método para calcular la mediana, depende si el total de los datos es par o impar. Por ejemplo, si son impares, solo se organizan de mayor a menor y se toma la tendencia central, dejando el mismo número en ambos extremos:

• Ejemplo:

Mediana de: 10, 12, 13, 15 y 9 = 9, 10, 12, 13, 15.

En este caso específico la mediana es el número 12.

Ahora bien, si se trata de elementos pares, se organiza igual de menor a mayor y se toman los elementos centrales para sumarlos.

• Ejemplo:

Mediana de: 7, 5, 2 y 8 = 2, 5, 7, 8.

Ahora se toman los dos elementos centrales y se suman. Por lo tanto la mediana es 5 + 7 = 12.

Moda

En cuanto a la moda, en los datos estadísticos pueden existir casos bimodales, multimodales o amodales. Esto quiere decir, que son los datos que se repiten con una frecuencia o que, por el contrario, no se llegan a repetir.

Ejemplo:

En este conjunto de datos 2, 5, 3, 4, 5 7, 9, se tiene que la 5 es la moda.

Pero en este conjunto 3, 4, 5, 7, 10, no hay moda o datos repetitivos, por lo que se considera amodal.

Referencias

• Cobo, B., & Díaz, C. (2003). Media, mediana y moda ¿Qué significa esto para los estudiantes de secundaria. In 27 Congreso Nacional de Estadística e Investigación Operativa. Disponible en: http://www.ugr.es/~batanero/pages/ARTICULOS/SEIOCobo2003.pdf
• García, A y otros (2014). Cuadernos de trabajo, facultad de estudios estadísticos. Universidad Complutense de Madrid. https://estudiosestadisticos.ucm.es/data/cont/docs/12-2014-10-16-CT05_2014.pdf
• Parra, J. M. (1995). Estadística descriptiva e inferencial I. Recuperado de: http://www. academia. edu/download/35987432/